Project: Textures
Textured Materials
If you recall (or look at) the definition for the RayHit class, you might notice that we haven’t done anything with the u and v values so far. This will change now. So far, all our surfaces have consisted of a single color, but often we actually want to place an image (file) on a surface, which is exactly what a texture is. However, our objects are three-dimensional, while images are two-dimensional, so we will need some way to determine which pixel to use from the texture image when the ray hits a particular location on our object. Cue u and v. While image files may have different dimensions, it is easier if we talk about them in a fixed interval, in our case as being between 0 and 1. We say that the bottom left corner of the image has coordinates (u,v) = (0,0) and the top right corner has (u,v) = (1,1). Then, if we have any arbitrary u- and v-values, we can multiply them with the width and height, respectively, and round them to get the actual pixel to be used. PImage-objects have a get-method that returns the color of a pixel at given coordinates that does exactly that.
The only question that remains is then: How do we get u and v? Unfortunately, this depends on the primitive in question (“unfortunately”, because that means you have to add u and v-calculations to every primitive you support).
UV-Coordinates on Spheres
The way we assign UV-Coordinates on a sphere is similar to how we assign latitude and longitude to locations on Earth (which is, in first approximation, a sphere): We decide on an (arbitrary) equator, and prime meridian, and then determine degrees above and below the equator, and degrees from the prime meridian. We can actually calculate these quantities using the normal vector (which, if placed at the center of the sphere, points towards the impact point, after all). If we assume that the xy-plane is the equator, u is the angle the x and y coordinate describe on that plane, and v is the angle the normal vector rises above this plane. We need to normalize both of these values to lie between 0 and 1, though:
UV-Coordinates on Planes
For a plane, the determination of u and v-coordinates runs into a problem: The plane is infinite, our image is not. While we could use a non-linear mapping, like 1/(1+x) to restrict values to be in the range between 0 and 1, this will lead to very strangely distorted images. A better approach, and what we will do, is to tile the texture on the plane, i.e. we define a size that the image should cover, and after that size the image will just be repeated again. In other words, we lay a grid onto the plane, and fill each cell of that grid with a copy of the texture image. To determine this grid, we need a defined start point and an orientation. The way we defined planes was using a point on the plane and the normal vector, which gives us both: The start of the grid is at the given point, and the orientation is given by the normal vector and the global z direction (0,0,1). We can determine “r(ight)” and “u(p)” of the grid (i.e. the local x and y-coordinates) as:
Note: There is one special case, where the normal vector points exactly into the (global) z-direction. In that case, r would be undefined, and we use the global y-direction instead. Why would it be undefined? Basically, you are looking for three basis vectors that are orthogonal to each other (a so-called orthonormal basis), with n already given, but there would be infinitely many choices how to rotate the grid around n. In order to “anchor” the second dimension, we choose the global z-direction and say that r is orthogonal on that as well. However, if n and z are the same direction, we still have infinitely many possible rotations, which would lead to undefined r.
In any case, with our right and up vectors in hand (and normalized!), we can determine the coordinates of the impact point i on this grid (which we can then convert to u- and v-coordinates). What we want to know is, given a vector $\vec{d} = \vec{i} - \vec{p}$, i.e. the vector pointing from the center of the plane to the impact point, what are this vectors components in terms of the right and up directions. We can calculate this, by determining the projection of $\vec{d}$ onto $\vec{r}$ and $\vec{u}$:
These x and y-coordinates now tell use how far from p along the grid our impact point is, but what we want are u and v coordinates. First, divide the values by scale to scale them to the desired size of the texture image. Then, compute u = x - floor(x) and v = (-y) - floor(-y) to get the desired values between 0 and 1. (Note that we have to negate y, as the image/texture coordinates start in the top left corner)
UV-Coordinates on Triangles
In order to put textures on triangles, we have to assign a coordinate to each point on the triangle. There are two ways to do this, where the second one (described in the next section) builds on the first. Every point on a triangle can be described as an interpolation (a “mixture”) of the three vertices of the triangle:
\[p = \theta v_1 + \phi v_2 + \psi v_3\]Where $v_1, v_2$ and $v_3$ are the three vertices of the triangle. The values $\theta, \phi$ and $\psi$ have two interesting (for our purposes) properties: They are each between 0 and 1, and they sum up to 1. The first property basically tells us that we could just use e.g. $\theta$ as $u$ and $\phi$ as $v$, and this will indeed be our first approach. The second property gives us some insight into how we might calculate these values: The idea is to start at $v_1$ and move along the edge from $v_1$ to $v_2$. Then we move on a line that is parallel to the edge from $v_1$ to $v_3$. We can reach each possible point of the triangle this way, we just need to go far enough “right” (assuming $v_1$ is on the bottom left) and then move “up”:
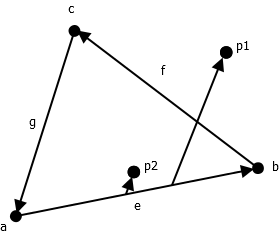
In this picture you can see how we can reach $p_1$ and $p_2$ in this way. Now, you might say $p_1$ is outside the triangle, and we only want points inside the triangle. This is where the second property mentioned above comes in: $\theta$ is the percentage of how far we move along the edge, and as we move further right, we can not move as far up anymore. For example, if $\theta=0.5$, we can only move at most halfway up the other edge (i.e. $phi$ will be at most $0.5$). The question remains how we calculate these values. Recall that one of the methods we discussed to determine if a point was in a triangle involved the following function:
ComputeUV(a, b, c, p)
e = b - a
g' = c - a
d = p - a
denom = e.e * g'.g' - e.g' * g'.e
u = (g'.g' * d.e - e.g' * d.g')/denom
v = (e.e * d.g' - e.g' * d.e)/denom
return (u,v)
To determine if the point was in the triangle, we would then check if they were both positive and summed up to less than 1. Why? Because this u is exactly our $\theta$ and this v is exactly our $\phi$. For now, you can just use them as $u$ and $v$, but in the next section we will see that this is not ideal.
UV-Coordinate Interpolation on Triangles
If you recall, one of the restrictions we placed on $\theta$ and $\phi$ was that they would add up to less than 1 (with the remainder being in $\psi$). What this means, if we use these values as texture coordinates, is that we will only ever use the bottom left half of a texture (i.e. we will put a diagonal from the top left corner to the bottom right corner and only use the pixels below this diagonal. Since images are rectangular, we are basically wasting half of the available space. On the other hand, if we have a more complex 3D model that consists of many triangles, it may be nice to be able to store all necessary texture information in a single file. Basically, we would like to be able to define which part of an image is mapped onto the triangle, and in this part you will do exactly this. Note that each of our triangles comes with three extra attributes tex1, tex2 and tex3 that correspond to the texture coordinates at the first, second and third vertex. To determine the texture coordinates of a given point, you use the equation:
Where $t_1, t_2$ and $t_3$ are tex1, tex2 and tex3. Note that the default value for tex1 is (1,0), the default value for tex2 is (0,1) and the default value for tex3 is (0,0), so with these default values your texture coordinates end up being:
And this is exactly what we used as our texture coordinates so far. However, if someone sets, for example, tex1 = (0.5, 0.5), tex2 = (0.75, 1) and tex3 = (1, 0.25), you would get:
Which results in $u = 0.5\theta + 0.75 \phi + \psi$ and $v = 0.5\theta + \phi + 0.25 \psi$. The practical result, though, is that the triangle will use the section of the image that corresponds to the triangle defined by the texture coordinates, and we can thus define an arbitrary piece of an image to be used for our triangle.
UV-Coordinates on other primitives (optional)
Unfortunately, the situation with texture coordinates is not well-defined for our other primitives, the quadrics. As they are (in our definition) all rotations around the z-axis, using the same scheme to determine the u-value that we also used for the sphere makes sense: The u-value depends on the angle the x and y coordinate describe on the horizontal plane. For the v-coordinate things are trickier, though, as our quadrics are infinite in height. We will therefore use the same scheme as for the plane and tile the texture (vertically). Like the plane, we have a scale-value (we only need one, since there is only one dimension to scale), and use this to determine how often the image should be repeated. As for the actual v-value to use, this can either be the z-coordinate directly (for cylinders and cones), or the square root of the z-coordinate (for paraboloids and hyperboloids), which counteracts some of the scaling issues we would otherwise have (placing a rectangular image on a hyperboloid will still look weird, but we are not going to be discussing these projections in this class).
Procedural Materials (optional)
Finally, recall that there is a third material type: Procedural materials. The basic idea behind a material is to determine a color value for given u and v coordinates, and in our raytracer this is done by calling a getColor(float u, float v)-method that e.g. loads a pixel from an image file. However, since we are already calling a function, we might as well just execute “arbitrary” code that computes the color value in some way. The reason why we might want to do this is to create (surface) animations, or graphical effects that change over time, or simply to apply a new effect to an existing image. The way procedural materials are implemented in the framework is via a (dynamic) factory, which can instantiate such a material given its name. In order to add a new procedural material, you need to implement two classes: The material itself (as a subclass of ProceduralMaterial) and a builder, as a subclass of ProceduralMaterialBuilder. Let’s start with the builder:
class LavaMaterialBuilder extends ProceduralMaterialBuilder
{
LavaMaterialBuilder()
{
super("Lava");
}
ProceduralMaterial make(MaterialProperties props)
{
return new LavaMaterial(props);
}
}
LavaMaterialBuilder lava = new LavaMaterialBuilder();
What the builder does is to call the super constructor with the name the material should be registered with (the super constructor will perform this registration, adding the builder to a dictionary using the name as the key). It also needs to implement a make method which actuall instantiates the material. Finally, there has to be an instance of the builder on the top level of the code. This will call the constructor, which will, in turn, register the builder in the registry.
The material itself does not need to concern itself with the factory or registration, and really just works like any other material:
class LavaMaterial extends ProceduralMaterial
{
PImage texture;
LavaMaterial(MaterialProperties props)
{
super(props);
this.texture = loadImage("lava.jpg");
this.texture.loadPixels();
}
color getColor(float u, float v)
{
u += sin(millis()/10000.0)/15;
v += sin(millis()/8000.0)/20;
int x = clamp(int(this.texture.width * u), 0, this.texture.width-1);
int y = clamp(int(this.texture.height*v), 0, this.texture.height-1);
return this.texture.get(x,y);
}
}
In this example, the material loads an image file ("lava.jpg") in its constructor, and to determine pixel to use for a surface, it will add a small, sine-based noise to the u and v-coordinates that depends on millis(), the number of milliseconds since the sketch was started. The effect of this is that the “lava” will “flow” (back and forth, with the offset following the sine-wave) on the surface of the object over time. The two example procedural materials only serve as a starting point. As you can write basically any code to determine a color, the possibilities of what can be done are endless. Note, though, that this code will run for every ray hit that is shown on the screen, i.e. the more complex the calculations are, the longer raytracing will take.
<!– Basically, we want to solve the following system of equations for x and y (p is the point/center the plane is defined by):
Since all our vectors have three dimensions, this gives use three equations for our two variables. If we choose the first two, we get (by letting $\vec{d} = \vec{i} - \vec{p}$):
\[x = \frac{(\vec{d} \times \vec{u})_z}{\vec{n}_z}\\ y = \frac{(\vec{l} \times \vec{d})_z}{\vec{n}_z}\]As you can see, if the z-component of the plane’s normal vector is 0, this will not work, but then you can use the y-component of the vectors. And if the y-component of the normal-vector is also 0, you can use the x-components. In any case, at least one of these three cases will work, since the impact point is guaranteed to be on the plane. –!>